Functions

The Concept of a Functions Pictorially

Explain the concept of a functions pictorially

Example

Explain the concept of a functions pictorially

Solution

It is not a function since 3 and 6 remain unmapped.
It is not a function because 2 has two images ( 5 and 6)
It is a function because each of 1, 2, 3 and 4 is connected to exactly one of 5, 6 or 7.

Functions

Identify functions

TESTING FOR FUNCTIONS:

If a line parallel to the y-axis is drawn and it passes through two or more points on the graph of the relation then the relation is not a function.

If it passes through only one point then the relation is a function

Example

Identify functions

Exercise

1. Which of the following relations are functions?

2. Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

and B ={ 2, 3, 5, 7 }

Draw an arrow diagram to illustrate the relation “ is a multiple of ‘ is it a function ? why?

3. let A = {1,-1 ,2,-2} and

B = {1, 2, 3, 4 } which of the following relations are functions ?

{ ( x , y ) : x < y }
{ ( x , y ) : x > y}
{ ( x , y ) : y = x2}

Domain and Range of a Function

The Domain of a Function

State the domain of a function

If y = f (x),that is y is a function of x ,then domain is a set of x values that satisfy the equation y = f (x).

The Range of Function

State the range of function

If y = f (x),that is y is a function of x , then therange is a set of y value satisfying the equation y = f (x).

Example

State the range of function

Solution

f (x) = y = 3x -5

When x = -2

f(-2) = y = 3x(-2)-5 = -11 , so (x,y)=(-2,-11)

f(3) =y= 3x3-5 = 4, so when x = 3 , y = 4

Therefore y is found in between – 11 and 4

Range ={ y: - 11≤ y≤ 4}

Example

State the range of function

Solutions;

Domain = all real numbers

Range:

f(x) = y = x2 – 3

Make x the subject

y+ 3 = x2

Exercise

1. For each of the following functions, state the domain and range

f(x) = 2x + 7 for 2 £ x £ 5
f(x) = x – 1 for -4 £ x £ 6
f(x) = 5 - 3x such that -2 £ f(x) < 8

2. for each of the following functions state the domain and range

f(x) = x2
f(x) = x2+2
f(x) = 2x + 1
f(x) = 1 – x2

Exercise

1.The range of the function

f(x) 3 – 2x for 0 ³0 x £7 is;

y: -18£ y £3
y: -3£ y £18
y: 3 £y £18
y: -18 £ y £-3

2. The range of the function

f(x)=2x+1 is y: -3£ y £17 what is the domain of this function?

x: - 3£ x £17
x: - 2£ x £8
x: -17 £ x £3

3.Which of the following relations represents a function:

R = (x, y) : y = for x ≥0
R= (x, y) : y2 = x-2 for x ≥0
R= (x, y) : y = for x ≥0 and y ≥0
R= (x, y) : x = 7 for all values of y

4.Which of the following relations is a function:

R = (x, y): -2 £ x £6, 3 £ y<8 and x<y, Where both x and y are integers
R= (x, y): -2 £ x £6, 3 £ y<8 and x<y, Where both x and y are integers
R= (x,y): y = √(x+2) for x ≥-2.
R = (x, y): y=√(2-x) for x ≤2 and y ≤0

5.Let f (x) = x2 + 1. Which of the following is true?

f (-2) < f (0)
f (3)> f (-4)
f (-5) = f (5)
The function crosses , y – axis at 1

One to one and many to one functions:

One to functions;

A one to one function is a function in which one element from the domain is mapped to exactly one element in the range:

That is if a ≠b then f (a) ≠f (b)

Many to one function;

This is another type of function with a property that two or more elements from the domain can have one image (the same image).

Examples of one to one functions

f (x) = 3x + 2
f (x) = x + 6
f (x) = x3 + 1 etc

Examples of many to one function

f(x) = x2 +1
f(x) = x4 – 2 etc

NB. All functions with odd degrees are one to one function and all functions with even degrees are many to one functions.

Example

State the range of function

Example

State the range of function

Q = {-1, 0, 1, 2, 3}

g(x) = x + 1, is g one to one function?

Solution:

g (x) is one to one function because every element in P has only one image in Q

NB: In example 1, f(x) is not a one to one function because -2 and 2 in A have the same image in B, that is 4 is the image of both 2 and -2.

Also 1 is the image of both 1 nd -1.

Example

State the range of function

Solution:

Draw a line parallel to the x axis and see if it crosses the graph at more than one points. If it does, then, the function is many to one and if it crosses at only one point then the graph represents a one to one function.

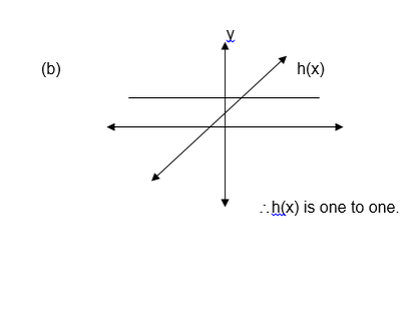
Graphic Function

Graphs of Functions

Draw graphs of functions

Many functions are given as equations, this being the case, drawing a graph of the equation is obtaining the graph of the equation which defines the function.

Note that, you can draw a graph of a function if you know the limits of its independent variables as well as dependent variables. i.e you must know the domain and range of the given function.

Example

Draw graphs of functions

f(x) = 3x -1
g (x) = x2 – 2x -1
h (x) = x3

Solution

f(x) = 3x – 1

The domain and range of f are the sets of all real numbers

f(x) = y = 3x – 1

So y = 3x – 1

Table of value :

g(x) = x2 -2x -1

y=x2-2-1

a=-1, b=-2 1 and c=-1

forh(x) = x3

Solution:

The first graph is the graph of linear function, the second one is called the graph of a quadratic function and the last graph is for cubic function.

Example

Draw graphs of functions

f(x) = -1 + 6x-x2

Solution:

a=-1, b=6, c=-1

Exercise

1.Which of the following are one to one function?

f(x) = 3x – x2
g (x) = x-1
k(x) =x3+1
f(x) =x+x2+x3
k(x)=x4

2. Draw the graph of the following functions:

f(x) = 3x – x2
h (x) = x+1
g(x) =x 3- x 2+3

3. At what values of x does the graph of the function f(x) = x2+x-6 cross thex- axis?

x=-3 and x=7
x=8 and x=-6
x=-3 and x=2
x=4 and x=-1

4. Which of the following function is one to one function?

f(x)=x2+2
f(x) =x4-x2
f(x)=x5-7
f(x)=x2+x+2

Functions with more than one part.

Some functions consist of more than one part. When drawing their graphs draw the parts separately.

If the graph includes an end point, indicate it with a solid dot if it does not include the end point indicate it with a hollow dot.

E.g. draw the graphs of the functions

(a) F(x) x+1 for x>0

(b) f(x)=x+1for x³0

Example

Draw graphs of functions

(d) State the domain and range of f

Solution:

Exercise

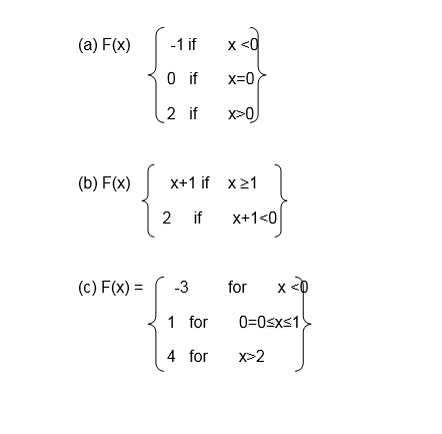
Absolute value functions (Modulus functions)

The absolute function is defined

Table of values

Example

Draw graphs of functions

Solution

table of values.

Step functions:

Example

Draw graphs of functions

Note that the graph obtained is like steps such functions are called steps functions

Exercise

1. Draw the graph of

Inverse of a Function

The Inverse of a Function

Explain the inverse of a function

In the discussion about relation we defined the inverse of relation.

It is true that the inverse of the relation is also a relation.

Similarly because a function is also relation then every function has its inverse

The Inverse of a Function Pictorially

Show the inverse of a function pictorially

According to the definition of function the inverse of a function is also a function if and only if the function is one to one

The Inverse of a Function

Find the inverse of a function

If the function f is one to one function given by an equation, then its inverse is denoted by f-1 which is obtained by inter changing the variables x and y then making y the subject of the formula.

I.e. If y=f(x), then x = f-1 (y)

Example

Find the inverse of a function